最小二乘法
最小二乘法是数据拟合中非常基础的一个方法。虽然它非常简单,然而同一种算法,每个人观察、学习的侧面却不尽相同。因此,我想还是有必要把我对最小二乘法的认识整理在这里。
数据拟合中最简单的是线性拟合的问题。比如,现在有这样采样的数据:
我们希望通过线性拟合来达到如下的效果:
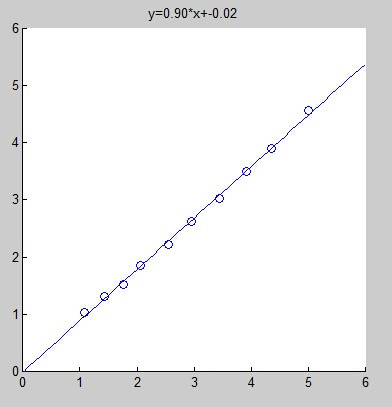
我们将这些数据点定义为$(x_1,y_1),(x_2,y_2),…,(x_N,y_N)$。并设该拟合出的直线为
$$ f(x)=a\times x+b $$
那么,我们肯定希望,这些离散的点离直线越近越好。写成数学表达式,即为:
$$ \min E(a,b) $$
其中,
$$ E(a,b) = \sum_{n=1}^{N}(y_n-(a\cdot x_n+b))^2 $$
矩阵形式解法
最小二乘法的提法就是这样。接下来就是要利用这个式子来求解参数$a$和参数$b$。由于我个人喜欢矩阵的简洁,因此,想方设法将上面的式子写成矩阵的形式。
$$ E(a,b) = \lVert { \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{pmatrix} - \begin{pmatrix} x_1 & 1 \\ x_2 & 1 \\ \vdots & \vdots \\ x_N & 1 \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix}} \rVert_2^2 $$
将关于$y$的向量用$\mathbf{y}$标记;关于$x$的矩阵用$\mathbf{X}$标记;关于参数的那个向量,我们用$\mathbf{\alpha}$标记。则最小二乘问题转换为:
$$ \min_{\mathbf{\alpha}} {\lVert \mathbf{y} - \mathbf{X}\mathbf{\alpha}\rVert}_2^2 $$
其中,$\mathbf{y}$和$\mathbf{X}$都是已知量,$\mathbf{\alpha}$是未知量,这种表示不太符合人的习惯。因此我做了一下字幕的替换。把$\mathbf{X}$替换成$\mathbf{A}$,把$\mathbf{\alpha}$替换成$\mathbf{x}$。此时,问题就变的比较好看了。
$$ \min_{\mathbf{x}} {\lVert \mathbf{y} - \mathbf{A}\mathbf{x}\rVert}_2^2 $$
下面我们要做的就是求解上式。方法很简单,求导,并且令导数为0。即:
$$ -2\mathbf{A^Ty}-2\mathbf{A^TAx}=0 $$
故
$$ \mathbf{x} = (\mathbf{A^TA})^{-1}\mathbf{A^Ty} $$
那么最小二乘法是否只能用来做线性拟合呢?其实并非如此。只要是对于参数而言是线性的都可以。例如多项式拟合:
$$ f(x) = a_nx^n+a_{n-1}x^{n-1} +\cdots+a_1x^1+a_0 $$
时刻要记住我们要求的是$a_0, a_1, \cdots , a_n$这些参数,而不是$x$。在上式中,参数的最高次就是1次。因此完全可以用最小二乘法来解决问题。
不过,当拟合的模式选择不正确时,很有可能导致欠拟合(under-fitting)或过拟合(over-fitting)。下面的图是当给出同一组数据时,分别选用线性拟合、二次拟合、4次拟合、8次拟合而得到的拟合曲线。其实,从直观上来看,我们不好判断线性拟合是不是欠拟合,但我们几乎可以肯定的说,8次拟合是过拟合了。


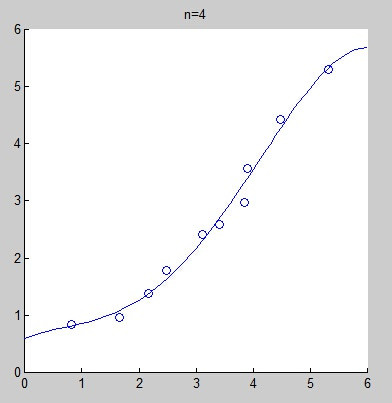
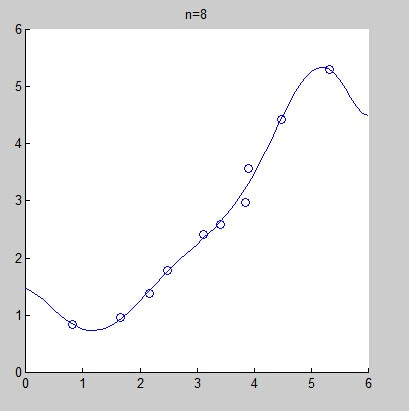
当然,我们可以通过增加一个约束项来解决所谓的过拟合问题。即:
$$ \min_{\mathbf{x}} {\lVert \mathbf{y} - \mathbf{A}\mathbf{x}\rVert}_2^2 + {\alpha \lVert \mathbf{x} \rVert}_2^2 $$
具体的原理很简单,不论是机器学习的教材也好,工程优化的教材也好,都会讲的很详细,这里就不展开说明了。上式对$\mathbf{x}$求导,可得
$$ -2\mathbf{A^Ty}+2\mathbf{A^TAx}+2\alpha\mathbf{Ix} $$
令上式为0,可得
$$ \mathbf{x} = (\mathbf{A^TA}+\alpha\mathbf{I})^{-1}\mathbf{A^Ty} $$
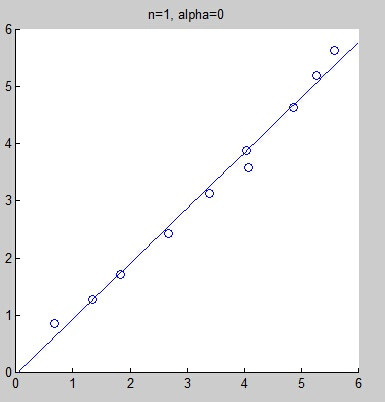
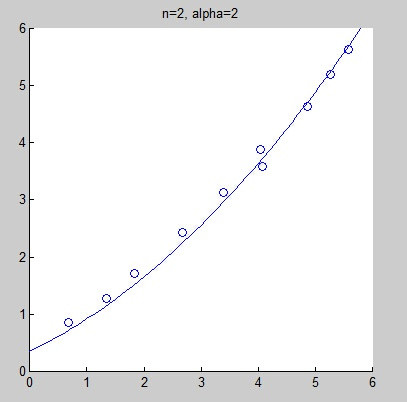
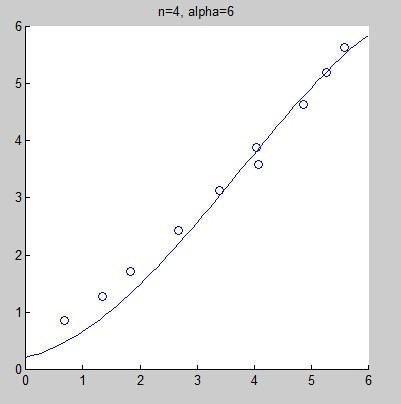
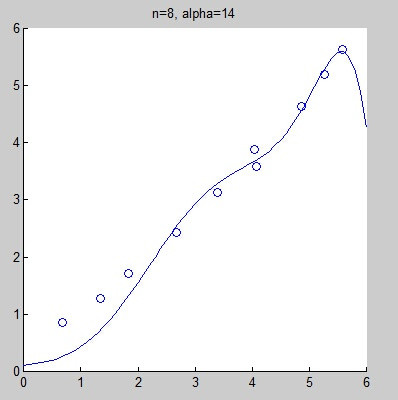
可以看到,结果有所改进。但也确实未必能解决所有的问题。
非矩阵解法
矩阵的解法比较炫,把问题归摄到一个很简单的方程式中。矩阵的编程,在C++中,一般推荐两个库。一个是如果已经在使用图像处理库了,那就可以直接使用OpenCV的Mat类,另外一个库更加小巧,专门用于矩阵计算的,叫Eigen。但如果在DSP的编程中,我们或许不需要这么炫,我们只要它快就可以了。 回顾一下,我们现在要解决的,是直线拟合的问题。也就是$y=kx+b$的问题。最小二乘法对应的目标函数如下:
$$ f(k,b) = \sum_i{(y_i-kx_i-b)^2} $$
我们想知道什么时候$f$能够取得最小值呢?那就做个导数吧:
$$ \frac{\partial{f(k,b)}}{\partial{k}}=-2\sum_i{(y_i-kx_i-b)x_i} $$
$$ \frac{\partial{f(k,b)}}{\partial{b}}=-2\sum_i{(y_i-kx_i-b)} $$
下面呢,自然就是让导数为0来求极值了。
$$ \sum_i{(y_i-kx_i-b)x_i} = 0 $$
$$ \sum_i{(y_i-kx_i-b)} = 0 $$
最后得到结果:
$$ k=\frac{n\sum_i^n{x_iy_i}-\sum_i^n{x_i}\sum_i^n{y_i}}{n\sum_i^n{x_i^2-(\sum_i^n{x_i})^2}} $$
$$ b=\frac{\sum_i^n{y_i}}{n}-k\frac{\sum_i^n{x_i}}{n} $$
带权值的最小二乘法
目标函数如下:
$$ f(k,b) = \sum_i{w_i(y_i-kx_i-b)^2} $$
接着求导:
$$ \begin{align} \frac{\partial{f(k,b)}}{\partial{k}}&=-2\sum_i{w_i(y_i-kx_i-b)x_i} \\ \frac{\partial{f(k,b)}}{\partial{b}}&=-2\sum_i{w_i(y_i-kx_i-b)} \end{align} $$
接着令导数为0,并且求$k$和$b$
$$ k=\frac{\sum_i{w_i}\sum_i{w_ix_iy_i}-\sum_i{w_ix_i}\sum_i{w_iy_i}}{\sum_i{w_i}\sum_i{w_ix_i^2}+\sum_i{w_i^2x_i^2}} $$
$$ b=\frac{\sum_i{w_iy_i}-k\sum{w_ix_i}}{\sum_i{w_i}} $$
如果写成矩阵形式,那就是类似于
$$ \min_{\mathbf{x}} (\mathbf{y} - \mathbf{A}\mathbf{x})^T\mathbf{W}(\mathbf{Ax}-\mathbf{y}) $$ 其中W为对角矩阵。
最终的解为: $$ \mathbf{x}=(\mathbf{A}^T\mathbf{WA})^{-1}\mathbf{AWy} $$